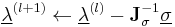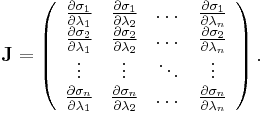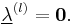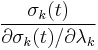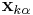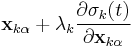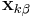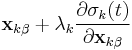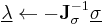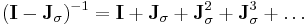Constraint algorithm
In mechanics, a constraint algorithm is a method for satisfying constraints for bodies that obey Newton's equations of motion. There are three basic approaches to satisfying such constraints: choosing novel unconstrained coordinates ("internal coordinates"), introducing explicit constraint forces, and minimizing constraint forces implicitly by the technique of Lagrange multipliers or projection methods.
Constraint algorithms are often applied to molecular dynamics simulations. Although such simulations are sometimes carried out in internal coordinates that automatically satisfy the bond-length and bond-angle constraints, they may also be carried out with explicit or implicit constraint forces for the bond lengths and bond angles. Explicit constraint forces typically shorten the time-step significantly, making the simulation less efficient computationally; in other words, more computer power is required to compute a trajectory of a given length. Therefore, internal coordinates and implicit-force constraint solvers are generally preferred.
Contents |
Mathematical background
The motion of a set of N particles can be described by a set of second-order ordinary differential equations, Newton's second law, which can be written in matrix form
where M is a mass matrix and q is the vector of generalized coordinates that describe the particles' positions. For example, the vector q may be a 3N Cartesian coordinates of the particle positions rk, where k runs from 1 to N; in the absence of constraints, M would be the 3Nx3N diagonal square matrix of the particle masses. The vector f represents the generalized forces and the scalar V(q) represents the potential energy, both of which are functions of the generalized coordinates q.
If M constraints are present, the coordinates must also satisfy M time-independent algebraic equations
where the index j runs from 1 to M. For brevity, these functions gi are grouped into an M-dimensional vector g below. The task is to solve the combined set of differential-algebraic (DAE) equations, instead of just the ordinary differential equations (ODE) of Newton's second law.
This problem was studied in detail by Joseph Louis Lagrange, who laid out most of the methods for solving it.[1] The simplest approach is to define new generalized coordinates that are unconstrained; this approach eliminates the algebraic equations and reduces the problem once again to solving an ordinary differential equation. Such an approach is used, for example, in describing the motion of a rigid body; the position and orientation of a rigid body can be described by six independent, unconstrained coordinates, rather than describing the positions of the particles that make it up and the constraints among them that maintain their relative distances. The drawback of this approach is that the equations may become unwieldy and complex; for example, the mass matrix M may become non-diagonal and depend on the generalized coordinates.
A second approach is to introduce explicit forces that work to maintain the constraint; for example, one could introduce strong spring forces that enforce the distances among mass points within a "rigid" body. The two difficulties of this approach are that the constraints are not satisfied exactly, and the strong forces may require very short time-steps, making simulations inefficient computationally.
A third approach is to use a method such as Lagrange multipliers or projection to the constraint manifold to determine the coordinate adjustments necessary to satisfy the constraints. Finally, there are various hybrid approaches in which different sets of constraints are satisfied by different methods, e.g., internal coordinates, explicit forces and implicit-force solutions.
Internal coordinate methods
The simplest approach to satisfying constraints in energy minimization and molecular dynamics is to represent the mechanical system in so-called internal coordinates corresponding to unconstrained independent degrees of freedom of the system. For example, the dihedral angles of a protein are an independent set of coordinates that specify the positions of all the atoms without requiring any constraints. The difficulty of such internal-coordinate approaches is twofold: the Newtonian equations of motion become much more complex and the internal coordinates may be difficult to define for cyclic systems of constraints, e.g., in ring puckering or when a protein has a disulfide bond.
The original methods for efficient recursive energy minimization in internal coordinates were developed by Gō and coworkers.[2][3]
Efficient recursive, internal-coordinate constraint solvers were extended to molecular dynamics.[4][5] Analogous methods were applied later to other systems.[6][7][8]
Lagrange multiplier-based methods
In most molecular dynamics simulation, constraints are enforced using the method of Lagrange multipliers. Given a set of n linear (holonomic) constraints at the time t,
where 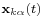 and
and 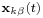 are the positions of the two particles involved in the kth constraint at the time t and
are the positions of the two particles involved in the kth constraint at the time t and 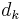 is the prescribed inter-particle distance.
is the prescribed inter-particle distance.
These constraint equations, are added to the potential energy function in the equations of motion, resulting in, for each of the N particles in the system
Adding the constraint equations to the potential does not change it, since all 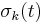 should, ideally, be zero.
should, ideally, be zero.
Integrating both sides of the equations of motion twice in time yields the constrained particle positions at the time 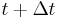
where 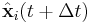 is the unconstrained (or uncorrected) position of the ith particle after integrating the unconstrained equations of motion.
is the unconstrained (or uncorrected) position of the ith particle after integrating the unconstrained equations of motion.
To satisfy the constraints 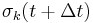 in the next timestep, the Lagrange multipliers must be chosen such that
in the next timestep, the Lagrange multipliers must be chosen such that
This implies solving a system of  non-linear equations
non-linear equations
simultaneously for the  unknown Lagrange multipliers
unknown Lagrange multipliers 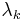 .
.
This system of  non-linear equations in
non-linear equations in  unknowns is best solved using Newton's method where the solution vector
unknowns is best solved using Newton's method where the solution vector 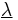 is updated using
is updated using
where 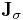 is the Jacobian of the equations σk:
is the Jacobian of the equations σk:
Since not all particles are involved in all constraints, 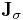 is blockwise-diagonal and can be solved blockwise, i.e. molecule for molecule.
is blockwise-diagonal and can be solved blockwise, i.e. molecule for molecule.
Furthermore, instead of constantly updating the vector 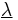 , the iteration is startedwith
, the iteration is startedwith 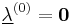 , resulting in simpler expressions for
, resulting in simpler expressions for 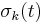 and
and 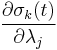 . After each iteration, the unconstrained particle positions are updated using
. After each iteration, the unconstrained particle positions are updated using
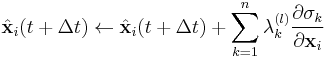 .
.
The vector is then reset to
This is repeated until the constraint equations 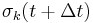 are satisfied up to a prescribed tolerance.
are satisfied up to a prescribed tolerance.
Although there are a number of algorithms to compute the Lagrange multipliers, they differ only in how they solve the system of equations, usually using Quasi-Newton methods.
The SETTLE algorithm
The SETTLE algorithm[9] solves the system of non-linear equations analytically for 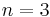 constraints in constant time. Although it does not scale to larger numbers of constraints, it is very often used to constrain rigid water molecules, which are present in almost all biological simulations and are usually modelled using three constraints (e.g. SPC/E and TIP3P water models).
constraints in constant time. Although it does not scale to larger numbers of constraints, it is very often used to constrain rigid water molecules, which are present in almost all biological simulations and are usually modelled using three constraints (e.g. SPC/E and TIP3P water models).
The SHAKE algorithm
The SHAKE algorithm was the first algorithm developed to satisfy bond geometry constraints during molecular dynamics simulations.[10]
It solves the system of non-linear constraint equations using the Gauss-Seidel method to approximate the solution of the linear system of equations
in the Newton iteration. This amounts to assuming that 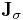 is diagonally dominant and solving the
is diagonally dominant and solving the  th equation only for the
th equation only for the  unknown. In practice, we compute
unknown. In practice, we compute
for all 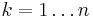 iteratively until the constraint equations
iteratively until the constraint equations 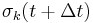 are solved to a given tolerance.
are solved to a given tolerance.
Each iteration of the SHAKE algorithm costs 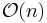 operations and the iterations themselves converge linearly.
operations and the iterations themselves converge linearly.
A noniterative form of SHAKE was developed later.[11]
Several variants of the SHAKE algorithm exist. Although they differ in how they compute or apply the constraints themselves, the constraints are still modelled using Lagrange multipliers which are computed using the Gauss-Seidel method.
The original SHAKE algorithm is limited to mechanical systems with a tree structure, i.e., no closed loops of constraints. A later extension of the method, QSHAKE (Quaternion SHAKE) was developed to amend this.[12] It works satisfactorily for rigid loops such as aromatic ring systems but fails for flexible loops, such as when a protein has a disulfide bond.[13]
Further extensions include RATTLE,[14] WIGGLE[15] and MSHAKE.[16] RATTLE works the same way as SHAKE,[17] yet using the Velocity Verlet time integration scheme. WIGGLE extends SHAKE and RATTLE by using an initial estimate for the Lagrange multipliers 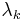 based on the particle velocities. Finally, MSHAKE computes corrections on the constraint forces, achieving better convergence.
based on the particle velocities. Finally, MSHAKE computes corrections on the constraint forces, achieving better convergence.
A final modification is the P-SHAKE algorithm[18] for rigid or semi-rigid molecules. P-SHAKE computes and updates a pre-conditioner which is applied to the constraint gradients before the SHAKE iteration, causing the Jacobian 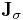 to become diagonal or strongly diagonally dominant. The thus de-coupled constraints converge much faster (quadratically as opposed to linearly) at a cost of
to become diagonal or strongly diagonally dominant. The thus de-coupled constraints converge much faster (quadratically as opposed to linearly) at a cost of 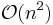 .
.
The M-SHAKE algorithm
The M-SHAKE algorithm[19] solves the non-linear system of equations using Newton's method directly. In each iteration, the linear system of equations
is solved exactly using an LU decomposition. Each iteration costs 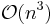 operations, yet the solution converges quadratically, requiring fewer iterations than SHAKE.
operations, yet the solution converges quadratically, requiring fewer iterations than SHAKE.
This solution was first proposed in 1986 by Ciccotti and Ryckaert[20] under the title "the matrix method", yet differed in the solution of the linear system of equations. Ciccotti and Ryckaert suggest inverting the matrix 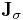 directly, yet doing so only once, in the first iteration. The first iteration then costs
directly, yet doing so only once, in the first iteration. The first iteration then costs 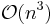 operations, whereas the following iterations cost only
operations, whereas the following iterations cost only 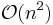 operations (for the matrix-vector multiplication). This improvement comes at a cost though, since the Jacobian is no longer updated, convergence is only linear, albeit at a much faster rate than for the SHAKE algorithm.
operations (for the matrix-vector multiplication). This improvement comes at a cost though, since the Jacobian is no longer updated, convergence is only linear, albeit at a much faster rate than for the SHAKE algorithm.
Several variants of this approach based on sparse matrix techniques were studied by Barth et al..[21]
The LINCS algorithm
An alternative constraint method, LINCS (Linear Constraint Solver) was developed in 1997 by Hess, Bekker, Berendsen and Fraaije,[22] and was based on the 1986 method of Edberg, Evans and Morriss (EEM),[23] and a modification thereof by Baranyai and Evans (BE).[24]
LINCS applies Lagrange multipliers to the constraint forces and solves for the multipliers by using a series expansion to approximate the inverse of the Jacobian 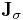 :
:
in each step of the Newton iteration. This approximation only works for matrices with Eigenvalues smaller than 1, making the LINCS algorithm suitable only for molecules with low connectivity.
LINCS has been reported to be 3-4 times faster than SHAKE.[22]
Hybrid methods
Hybrid methods have also been introduced in which the constraints are divided into two groups; the constraints of the first group are solved using internal coordinates whereas those of the second group are solved using constraint forces, e.g., by a Lagrange multiplier or projection method.[25][26][27] This approach was pioneered by Lagrange,[1] and result in Lagrange equations of the mixed type.[28]
See also
References and footnotes
- ^ a b Laplace, PS (1788). Mécanique analytique.
- ^ Noguti T, Toshiyuki; Gō N (1983). "A Method of Rapid Calculation of a 2nd Derivative Matrix of Conformational Energy for Large Molecules". Journal of the Physical Society of Japan 52 (10): 3685–3690. doi:10.1143/JPSJ.52.3685.
- ^ Abe, H; Braun W, Noguti T, Gō N (1984). "Rapid Calculation of 1st and 2nd Derivatives of Conformational Energy with respect to Dihedral Angles for Proteins: General Recurrent Equations". Computers and Chemistry 8 (4): 239–247. doi:10.1016/0097-8485(84)85015-9.
- ^ Bae, D-S; Haug EJ (1988). "A Recursive Formulation for Constrained Mechanical System Dynamics: Part I. Open Loop Systems". Mechanics of Structures and Machines 15: 359–382.
- ^ Jain, A; Vaidehi N, Rodriguez G (1993). "A Fast Recursive Algorithm for Molecular Dynamics Simulation". Journal of Computational Physics 106 (2): 258–268. Bibcode 1993JCoPh.106..258J. doi:10.1006/jcph.1993.1106.
- ^ Rice, LM; Brünger AT (1994). "Torsion Angle Dynamics: Reduced Variable Conformational Sampling Enhances Crystallographic Structure Refinement". Proteins: Structure, Function, and Genetics 19 (4): 277–290. doi:10.1002/prot.340190403. PMID 7984624.
- ^ Mathiowetz, AM; Jain A, Karasawa N, Goddard III, WA (1994). "Protein Simulations Using Techniques Suitable for Very Large Systems: The Cell Multipole Method for Nonbond Interactions and the Newton-Euler Inverse Mass Operator Method for Internal Coordinate Dynamics". Proteins: Structure, Function, and Genetics 20 (3): 227–247. doi:10.1002/prot.340200304. PMID 7892172.
- ^ Mazur, AK (1997). "Quasi-Hamiltonian Equations of Motion for Internal Coordinate Molecular Dynamics of Polymers". Journal of Computational Chemistry 18 (11): 1354–1364. doi:10.1002/(SICI)1096-987X(199708)18:11<1354::AID-JCC3>3.0.CO;2-K.
- ^ Miyamoto, S; Kollman PA (1992). "SETTLE: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models". Journal of Computational Chemistry 13 (8): 952–962. doi:10.1002/jcc.540130805.
- ^ Ryckaert, J-P; Ciccotti G, Berendsen HJC (1977). "Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes". Journal of Computational Physics 23 (3): 327–341. Bibcode 1977JCoPh..23..327R. doi:10.1016/0021-9991(77)90098-5.
- ^ Yoneya, M; Berendsen HJC, Hirasawa K (1994). "A Noniterative Matrix Method for Constraint Molecular-Dynamics Simulations". Molecular Simulations 13 (6): 395–405. doi:10.1080/08927029408022001.
- ^ Forester, TR; Smith W (1998). "SHAKE, Rattle, and Roll: Efficient Constraint Algorithms for Linked Rigid Bodies". Journal of Computational Chemistry 19: 102–111. doi:10.1002/(SICI)1096-987X(19980115)19:1<102::AID-JCC9>3.0.CO;2-T.
- ^ McBride, C; Wilson MR, Howard JAK (1998). "Molecular dynamics simulations of liquid crystal phases using atomistic potentials". Molecular Physics 93 (6): 955–964. doi:10.1080/002689798168655.
- ^ Andersen, Hans C. (1983). "RATTLE: A "Velocity" Version of the SHAKE Algorithm for Molecular Dynamics Calculations". Journal of Computational Physics 52: 24–34. doi:10.1016/0021-9991(83)90014-1.
- ^ Lee, Sang-Ho; Kim Palmo, Samuel Krimm (2005). "WIGGLE: A new constrained molecular dynamics algorithm in Cartesian coordinates". Journal of Computational Physics 210: 171–182. doi:10.1016/j.jcp.2005.04.006.
- ^ Lambrakos, S. G.; J. P. Boris, E. S. Oran, I. Chandrasekhar, M. Nagumo (1989). "A Modified SHAKE algorithm for Maintaining Rigid Bonds in Molecular Dynamics Simulations of Large Molecules". Journal of Computational Physics 85 (2): 473–486. doi:10.1016/0021-9991(89)90160-5.
- ^ Leimkuhler, Benedict; Robert Skeel (1994). "Symplectic numerical integrators in constrained Hamiltonian systems". Journal of Computational Physics 112: 117–125. doi:10.1006/jcph.1994.1085.
- ^ Gonnet, Pedro (2007). "P-SHAKE: A quadratically convergent SHAKE in
 ". Journal of Computational Physics 220 (2): 740–750. doi:10.1016/j.jcp.2006.05.032.
". Journal of Computational Physics 220 (2): 740–750. doi:10.1016/j.jcp.2006.05.032. - ^ Kräutler, Vincent; W. F. van Gunsteren, P. H. Hünenberger (2001). "A Fast SHAKE Algorithm to Solve Distance Constraint Equations for Small Molecules in Molecular Dynamics Simulations". Journal of Computational Chemistry 22 (5): 501–508. doi:10.1002/1096-987X(20010415)22:5<501::AID-JCC1021>3.0.CO;2-V.
- ^ Ciccotti, G.; J. P. Ryckaert (1986). "Molecular Dynamics Simulation of Rigid Molecules". Computer Physics Reports 4 (6): 345–392. doi:10.1016/0167-7977(86)90022-5.
- ^ Barth, Eric; K. Kuczera, B. Leimkuhler, R. Skeel (1995). "Algorithms for constrained molecular dynamics". Journal of Computational Chemistry 16 (10): 1192–1209. doi:10.1002/jcc.540161003.
- ^ a b Hess, B; Bekker H, Berendsen HJC, Fraaije JGEM (1997). "LINCS: A Linear Constraint Solver for Molecular Simulations". Journal of Computational Chemistry 18 (12): 1463–1472. doi:10.1002/(SICI)1096-987X(199709)18:12<1463::AID-JCC4>3.0.CO;2-H.
- ^ Edberg, R; Evans DJ, Morriss GP (1986). "Constrained Molecular-Dynamics Simulations of Liquid Alkanes with a New Algorithm". Journal of Chemical Physics 84 (12): 6933–6939. doi:10.1063/1.450613.
- ^ Baranyai, A; Evans DJ (1990). "New Algorithm for Constrained Molecular-Dynamics Simulation of Liquid Benzene and Naphthalene". Molecular Physics 70: 53–63. doi:10.1080/00268979000100841.
- ^ Mazur, AK (1999). "Symplectic integration of closed chain rigid body dynamics with internal coordinate equations of motion". Journal of Chemical Physics 111 (4): 1407–1414. doi:10.1063/1.479399.
- ^ Bae, D-S; Haug EJ (1988). "A Recursive Formulation for Constrained Mechanical System Dynamics: Part II. Closed Loop Systems". Mechanics of Structures and Machines 15: 481–506.
- ^ Rodriguez, G; Jain A, Kreutz-Delgado K (1991). "A Spatial Operator Algebra for Manipulator Modeling and Control". The International Journal for Robotics Research 10 (4): 371–381. doi:10.1177/027836499101000406.
- ^ Sommerfeld, Arnold (1952). Lectures on Theoretical Physics, Vol. I: Mechanics. New York: Academic Press. ISBN 0126546703.
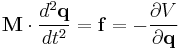
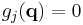
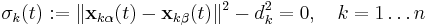
![\frac{\partial^2 \mathbf x_i(t)}{\partial t^2} m_i = -\frac{\partial}{\partial \mathbf x_i} \left[ V(\mathbf x_i(t)) %2B \sum_{k=1}^n \lambda_k \sigma_k(t) \right], \quad i=1 \dots N.](/2012-wikipedia_en_all_nopic_01_2012/I/3ba6312c063dfd69e30c9107262791ca.png)
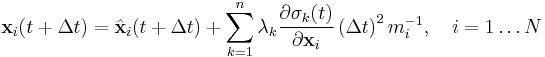
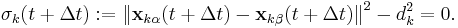
![\sigma_j(t %2B \Delta t)�:= \left\| \hat{\mathbf x}_{j\alpha}(t%2B\Delta t) - \hat{\mathbf x}_{j\beta}(t%2B\Delta t) %2B \sum_{k=1}^n \lambda_k \left[ \frac{\partial\sigma_k(t)}{\partial \mathbf x_{j\alpha}}m_{j\alpha}^{-1} - \frac{\partial\sigma_k(t)}{\partial \mathbf x_{j\beta}}m_{j\beta}^{-1}\right] \right\|^2 - d_j^2 = 0, \quad j = 1 \dots n](/2012-wikipedia_en_all_nopic_01_2012/I/d2e68dd614bc27ec15b6d2248c67191f.png)